Fracciones.

¿Qué es una fracción?

En el mundo de las matemáticas, la fracción es una expresión que marca una división, por lo tanto, se puede decir que una fracción representa un reparto o una porción de una unidad. La palabra fracción tiene su origen en el latín, específicamente la palabra “fractio”.

Partes de una fracción

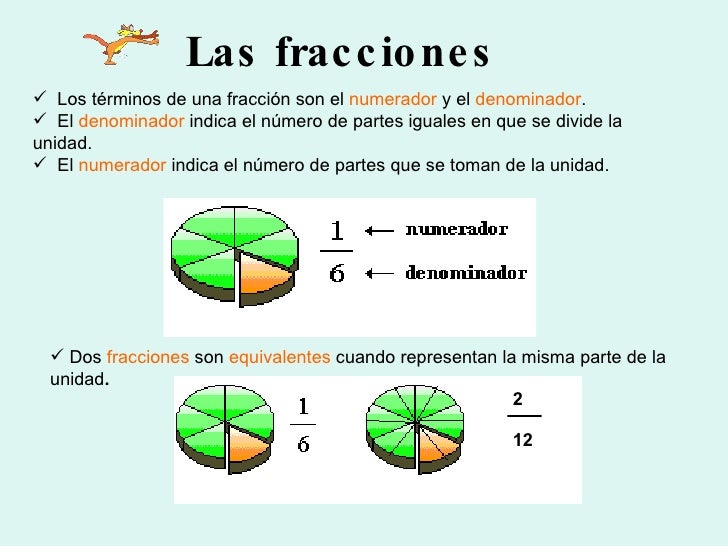
La fracción se compone especialmente de dos números, el número que está arriba de la línea se llama numerador y el número que está debajo de la línea se llama denominador.

2 ← numerador

3 ← denominador

Lectura de fracciones. El número que está en el numerador se lee tal y como conocemos al número, en el caso del denominador el nombre cambia y se debe considerar los siguientes nombramientos:

Nombramiento si el denominador va de 2 a 10:Si es 2 es "medios".

Si es 3 es "tercios".

Si es 4 es “cuartos”.

Si es 5 es “quintos”.

Si es 6 es “sextos”.

Si es 7 es “séptimo”.

Si es 8 es “octavos”.

Si es 9 es “novenos”.

Si es 10 es “décimos”.

Nombramiento si el denominador es superior a 10:

Se considera el nombre normal del número pero se le agrega al nombre la terminación “avos”, por ejemplo:

3/12 se puede leer como “tres doceavos”.

6/22 se puede leer como “seis veintedosavos”.

1/60 se puede leer como “sesentavos”.

Nombramiento si el denominador termina en 1 seguido solo de ceros:

Si es 10 es “décimos”.

Si es 100 es “centésimo”.

Si es 1 000 es “milésimo”.

Si es 10 000 es “diezmilésimo”.

Si es 100 000 es “cienmilésimo”.

Si es 1 000 000 es “"millonésimo”.

Por ejemplo: 7/1000 se puede leer como “siete milésimos”

Representación de fracciones

Una unidad se puede representar de diferentes formas, dependiendo de las particiones o secciones en que se divida. En las siguientes figuras se representa en azul la partición considerada. En la primera figura se hacen 2 particiones y se toma una porción, se puede leer como “un medio” (1/2). En la segunda figura se consideran 4 particiones y se toma una porción, se puede leer como “un cuarto” (1/4). En la tercera figura se considera 4 particiones y se toman 3 porciones, se puede leer como “tres cuartos” (3/4).

NOTA: Las fracciones resultan de repartir la misma cantidad de porciones a un número dado de objetos, personas, etcétera.

Y como siempre para ampliar tu conocimiento te dejo el siguiente video:

Figuras Geométricas.

¿Qué son las Figuras Geométricas?

Las figuras geométricas son superficies delimitadas por líneas (curvas o rectas) o espacios delimitados por superficies. En el primer caso, se está haciendo referencia a polígonos, círculos, circunferencias, elipses; y, en el segundo caso, se está hablando de poliedros.

Debemos destacar también la diferencia entre:

• Líneas curvas cerradas, que serían el círculo y la circunferencia.
• Líneas poligonales cerradas, que son los polígonos.
  
  
  Líneas
  
  Una línea es una sucesión de puntos en el espacio. Se clasifican en rectas y curvas.
  
  Son líneas rectas si todos los puntos van en la misma dirección.
  Son líneas curvas cuando los puntos cambian de dirección.

Circunferencia

Es la línea curva que encierra un trozo de un plano. Los elementos que forman una circunferencia son: el diámetro, el centro, el radio, la cuerda y el arco.

Círculo

Es el trozo de plano que encierra la circunferencia. Los elementos que forman un círculo son; el semicírculo, el sector circular y el segmento circular.

Ahora conoceremos los elementos de un polígono.

A los polígonos se les nombra según el número de sus lados, teniendo así:

Triángulos

Son los polígonos de tres lados. Se pueden clasificar:

Según sus lados: equilátero, isósceles y escaleno.

Según sus ángulos: equiángulo, acutángulo y obtusángulo.

Cuadriláteros

Son los polígonos de cuatro lados, se dividen entre paralelogramos y no paralelogramos.

Los paralelogramos son: el cuadrado, el rectángulo, el romboide y el rombo.

Los no paralelogramos son: el trapecio y el trapezoide.

Para ampliar tu conocimiento te dejo el siguiente video.

Recta Real.

La recta real​ o recta numérica es un gráfico unidimensional o línea recta la cual contiene todos los números reales ya sea mediante una correspondencia biunívoca o mediante una aplicación biyectiva, usada para representar los números como puntos especialmente marcados, por ejemplo los números enteros mediante una recta llamada recta graduada como la entera de ordenados y separados con la misma distancia.

Está dividida en dos mitades simétricas por el origen, es decir el número cero.

La recta numérica es una línea en la cual suelen graficarse los números enteros como puntos que están separados por una distancia uniforme. Nos permite localizar y comparar números así como realizar operaciones de suma y resta.

Más información.

Fracciones en la recta numérica. Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la fracción según indica el numerador. Como puedes observar las fracciones unitarias se ubican en el primer segmento de la recta numérica.

Es importante saber graficar fracciones en la recta numérica y por ello, te comparto el siguiente video.

 

CONCEPTO DE NÚMERO. 

En el aspecto de concepto de número incluimos las representaciones de los números cuando éstos no están asociados a ninguna operación ni al orden. Es de esperar que esto suceda en el momento de introducir un nuevo sistema numérico, pero no únicamente ahí. Estudiamos si las representaciones en la recta se usan para “colocar los números” (representar los números de manera aislada) o como apoyo para “estimar”.

Figura 1 Representación de la recta para colocar puntos.

Figura 2 Representación de la recta para estimar

Además, diferenciamos si los números se representan con puntos o con flechas y si las rectas usadas son horizontales, verticales o ejes cartesianos.

Figura 3 Representación de una suma con puntos-flecha

Figura 4 Representación de una suma con tres flechas.

SUMA Y RESTA.

En la suma y resta distinguimos si las representaciones utilizadas son del tipo puntos-flecha (véase figura 3) o del tipo tres flechas (véase figura 4). En ocasiones estas representaciones pueden venir acompañadas de un problema aditivo verbal. Por ello, también distinguimos el tipo de estructura de problema a la que se asocian. Los problemas aditivos que hemos analizado son los siguientes, adoptando la notación de Bruno y Martinón (1997): 

• Cambio: ei + v = ef (estado inicial + variación = estado final). “Un delfín estaba a 5 metros bajo el nivel del mar y bajó 8 metros. ¿Cuál era la posición del delfín después de este movimiento?” 

• Combinación: e1 + e2 = et (estado parcial 1 + estado parcial 2 = estado total). “Pedro tiene 8 pesetas y debe 15 pesetas. ¿Cuál es su situación económica total?” 

• Dos cambios: v1 + v2 = vt (variación primera + variación segunda = variación total). “La temperatura bajó 11 grados y luego subió 5 grados. ¿Cómo varió la temperatura con respecto a la que hacía antes de moverse?” 

• Comparación: e1 + c = e2 (estado menor + comparación = estado mayor). “Un coche está en el kilómetro 6 a la izquierda del cero y una moto está 11 kilómetros a la derecha del coche. ¿Cuál es la posición de la moto?”

Figura 5 Representación del producto como sumas reiteradas

Figura 6 Representación del producto como producto cartesiano.

PRODUCTO.

Para el producto distinguimos si las representaciones que se utilizan son de sumas reiteradas (véase figura 5) o bien de producto cartesiano (véase figura 6). Igual que en las sumas y las restas, estas representaciones pueden aparecer contextualizadas con problemas de multiplicación o división. Distinguimos si los problemas que aparecen son de: 

• Razón: “Tengo 42 sillas que quiero colocar en 7 filas del mismo tamaño. ¿Cuántas filas podré formar?” 

• Comparación: “Juan tiene 23 años y su abuelo tiene tres veces la edad de Juan. ¿Cuántos años tiene el abuelo de Juan?” 

• Producto cartesiano: “Tengo 4 blusas y 5 pantalones. ¿De cuántas maneras distintas me puedo vestir?”

Regla de Tres Simple.

La regla de tres simple es una herramienta matemática que sirve para resolver rápidamente problemas que involucran una relación de proporcionalidad directa entre dos variables. Por ejemplo: Una motocicleta recorre 320 kilómetros en 150 minutos, ¿a cuántos kilómetros por hora viajó?.

Para plantear de manera correcta una regla de tres simple se deben conocer tres datos, y solo uno es el que opera como incógnita: si A (valor conocido) mantiene con B (valor conocido) cierta relación, y se sabe que C (valor conocido) con D (valor desconocido y llamado por tal razón “incógnita”) guardan igual relación, es posible calcular el valor incógnita D usando los valores A, B y C.

Características de la regla de tres simple.

La forma de resolver la incógnita es muy sencilla y fácil de memorizar, de hecho es uno de los primeros razonamientos que se le enseña al niño durante la escolaridad primaria, donde comienzan a manejar las operaciones básicas (suma, resta, multiplicación y división).

Si se anotan los datos cuya relación positiva es conocida arriba, y debajo y encolumnado se anota, a un lado (generalmente por convención el izquierdo) el dato conocido de la otra serie.

La incógnita resultará de multiplicar los dos valores conocidos que se encuentran en diagonal, B x C, y dividir ese producto por el valor conocido restante, es decir A; así se obtendrá el valor incógnita D.

En la regla de tres simple se establece, por tanto, la relación de proporcionalidad entre dos valores conocidos A y B , y conociendo un tercer valor C, se calcula un cuarto valor D.

Dicha relación de proporcionalidad existente entre A y B puede ser directa o inversa.

Será directa cuando, dentro de esa proporcionalidad, a un mayor valor de A le corresponda también un mayor valor de B (o a un menor valor de A le corresponda un menor valor de B), y será inversa, cuando a un mayor valor de A le corresponda un menor valor de B (o a un menor valor de A le corresponda un mayor valor de B).

En el primer caso tenemos una regla de tres simple directa, y en el segundo caso una regla de tres simple inversa.

Vamos a ver cada una más detalladamente.

En la regla de tres simple directa, en la relación entre los valores, se cumple que:

y decimos que A es a B directamente proporcional, como C es a D.

De esta igualdad anterior, se deduce fácilmente que, por ejemplo, si conocemos los valores A, B y C, y queremos calcular D, éste último será:

Lo vemos con un ejemplo.

Julia tiene que comprar pintura blanca para darle una mano previa a una habitación que quiere cambiar de color. Si en el bote de pintura se indica que con 1 litro de pintura se pueden pintar 8 m2. ¿Cuántos litros necesita teóricamente para pintar las paredes de la habitación si ésta tiene 40 m2 de pared?

En este caso, la relación de proporcionalidad es directa, puesto que cuanto más metros cuadrados de pared tengamos que pintar más litros de pintura necesitaremos. Lo hacemos como hemos visto antes:

Julia necesitará, por tanto, 5 litros de pintura.

Para una mejor comprensión te comparto el siguiente video.

 En la regla de tres simple inversa, en la relación entre los valores, se cumple que:

y decimos que A es a B inversamente proporcional, como C es a D.

Conocidos los valores A, B y C, el valor D será:

Por ejemplo: «Un grifo con un caudal de salida de agua de 18 litros por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 litros por minuto?»

La relación de proporcionalidad es inversa, ya que cuanto más caudal de salida de agua tiene el grifo menos tiempo (en horas) se necesita para llenar el depósito. Tenemos así que:

Con un grifo de 7 litros por minuto de caudal (menos caudal) necesitamos 36 horas (más tiempo) para llenar el depósito.

Y como siempre, para una mejor comprensión te dejo el siguiente video:

Proporcionalidad directa.

En esta ocasión vamos a estudiar la proporcionalidad directa y  para que sirve. Pero antes necesitamos saber qué es una magnitud. Una magnitud es aquello que se puede medir. Por ejemplo, el peso de una persona, el número de albañiles trabajando, el número de plátanos, la cantidad de pienso que come un perro, la distancia entre dos pueblos o la velocidad de un caballo al galopar.

Todas estas magnitudes se pueden relacionar con otras.

Se puede relacionar:

• El peso de una persona con la talla de ropa que usa.
• El número de albañiles trabajando con el tiempo que tardan en terminar la obra.
• El número de plátanos con el número de cajas necesarias para colocarlos.
• La distancia entre dos pueblos con el tiempo que se tarda en ir de uno a otro.
• La velocidad de un caballo galopando con el tiempo que tarda el caballo en llegar de un punto a otro.

Hay varios tipos de relaciones. Hoy veremos solo una de ellas: la proporcionalidad directa.

Para que dos magnitudes mantengan una relación de proporcionalidad directa tienen que estar relacionadas de tal forma que si duplicamos una, la otra se tiene que duplicar, si la triplicamos la otra también y si la reducimos a la mitad la otra también se tiene que reducir. Se puede entender que si aumentamos la cantidad de una, la otra tiene que aumentar también proporcionalmente.

¿Qué relación podemos ver entre el número de plátanos y el número de cajas que necesitamos para guardarlos?

Podréis observar que cuantos más plátanos tenemos más cajas necesitamos, ¿verdad? Estas dos magnitudes mantienen una relación proporcionalmente directa.

Es importante saber que el cociente (razón o proporción) entre dos magnitudes directamente proporcionales es siempre constante. En nuestro ejemplo tenemos que la razón es 3.

Las relaciones de proporcionalidad aparecen con mucha frecuencia en nuestra vida cotidiana. Pero ya definido de una forma matemática daremos un concepto de la  proporcionalidad directa de la siguiente manera.

 ¿Qué es una proporcionalidad directa?

Dos variables x e y son directamente proporcionales o están en proporción directa si, al aumentar (o disminuir) una en cierto factor, la otra aumenta (o disminuye) en el mismo factor. Es decir, el cociente entre sus valores relacionados es constante. 

Lo anterior se puede representar con:

La expresión que modela la proporcionalidad directa es: y = k ∙ x, con x, y, k > 0 Toda proporción directa se puede representar en el plano cartesiano con una semirrecta que parte en el origen. Su inclinación (pendiente) dependerá de la constante de proporcionalidad.

Para que puedas ver mas a fondo la utilidad o aplicabilidad de la proporción directa te dejo el video siguiente.

 

MCM Y MCD.

 

Como todo lo que se estudia en matemáticas, los criterios de divisibilidad, así como el cálculo de los múltiplos, tienen gran importancia para la resolución de problemas que se presentan en la vida diaria.

Así que empecemos por los divisores de un número:

Ahora, que ya hemos conocido los divisores de un numero vamos a conocer algunos criterios de divisibilidad que son de gran importancia para poder entender este tema

Así, procedemos a calcular el MCM (mínimo común múltiplo) y MCD (máximo común divisor)

MAXIMO COMUN DIVISOR.

El máximo común divisor (m.c.d) de dos o mas números es el mayor de los divisores comunes.

Para hallar el máximo común divisor de dos o mas números, por ejemplo: m.c.d (12,18) se siguen los siguientes pasos:

1. Se descompone cada numero en producto de factores primos.
2. El producto de estos factores primos elevados al menor exponente es el máximo común divisor de los números dados.

MINIMO COMUN MULTIPLO.

El mínimo común múltiplo (m.c.m) de dos o mas números es el menor múltiplos común distinto de cero.

Para hallar el máximo común divisor de dos o mas números, por ejemplo: m.c.m (30,45) se siguen los siguientes pasos: 

1. Se descompone cada numero en producto de factores primos.
2. El producto de estos factores primos elevados al mayor exponente es el máximo común divisor de los números dados.

En muchas ocasiones se nos hace difícil saber identificar como y donde utilizar m.c.m o m.c.d, en vista de este error te dejare el siguiente video para que no tengas ese problema matemático. 

Números en la Vida Cotidiana.

Los números naturales son los que utilizamos en la vida cotidiana para contar u ordenar y pertenecen al conjunto de números enteros positivos.

El conjunto de los números naturales se representa por ℕ y está formado por: 

Nosotros consideramos que 0 es un número natural, aunque no todos los autores están de acuerdo.

Los números naturales no tienen decimal, unidad imaginaria, o bien no son fracciones.

Los números naturales son ilimitados, si a un número natural le sumamos 1, obtenemos otro número natural.

Algunas utilidades de los números naturales

1 Contar los elementos de un conjunto (número cardinal).

8 es el número de planetas del Sistema Solar.

2 Expresar la posición u orden que ocupa un elemento en un conjunto (número ordinal).

3 Identificar y diferenciar los distintos elementos de un conjunto.

Orden en los números

Los números naturales están ordenados, lo que nos permite comparar dos números naturales:

Ejemplo:

 

Como

y además: 

,

Relaciones de orden

Los números naturales sirven para establecer relaciones de orden del tipo mayor que, menor que o igual que.

Tanto la suma como la multiplicación de números naturales son operaciones que cumplen las propiedades conmutativa y asociativa. Es decir, el orden de los números naturales en una suma o multiplicación no alteran el producto obtenido (a + b = b + a y a x b = b x a).

También se cumple que para sumar o multiplicar más de dos números naturales, no es necesario agruparlos de una forma determinada; Por ejemplo, (a + b) + c = a + (b + c) = a +b + c.

En las matemáticas y la ciencia se utilizan los números naturales para tres propósitos principales:

Describir la posición de un elemento en una sucesión o secuencia.

Para determinar el tamaño de un conjunto finito.

Construir los números enteros (los números naturales, más los números negativos, más el cero).

El conjunto de los números naturales comienza con el uno y sigue una progresión aritmética donde a cada nuevo valor se le suma uno. Los números naturales se utilizan en el día a día para contar y enumerar cosas, así como para cálculos simples relacionados.

En las matemáticas, los números naturales permiten definir otros números, especificar el tamaño de un conjunto finito y describir la posición de un elemento en una secuencia ordenada.

Los números naturales se han utilizado a lo largo de la historia para contar y organizar, pero no fue hasta el siglo XIX cuando se definieron de forma precisa.

Y como siempre para afianzar mejor nuestro aprendizaje te dejo un video mas explicativo.