La recta real o recta numérica es un gráfico unidimensional o línea recta la cual contiene todos los números reales ya sea mediante una correspondencia biunívoca o mediante una aplicación biyectiva, usada para representar los números como puntos especialmente marcados, por ejemplo los números enteros mediante una recta llamada recta graduada como la entera de ordenados y separados con la misma distancia.
Está dividida en dos mitades simétricas por el origen, es decir el número cero.

La recta numérica es una línea en la cual suelen graficarse los números enteros como puntos que están separados por una distancia uniforme. Nos permite localizar y comparar números así como realizar operaciones de suma y resta.
Más información.
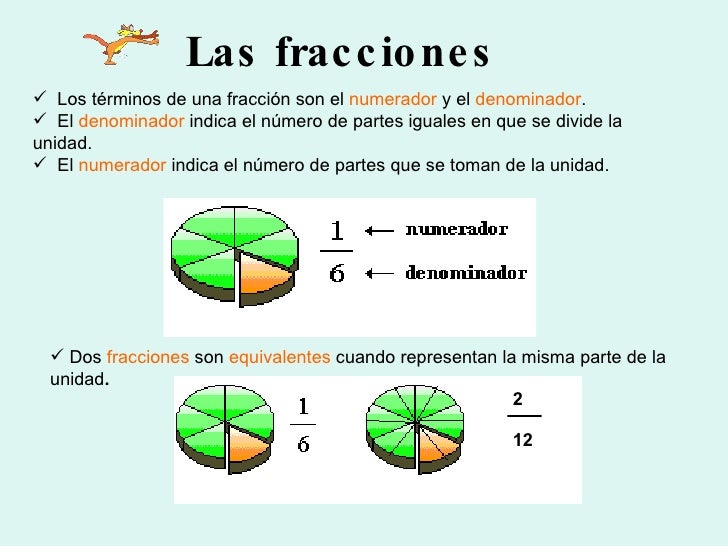
Fracciones en la recta numérica. Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la fracción según indica el numerador. Como puedes observar las fracciones unitarias se ubican en el primer segmento de la recta numérica.
Es importante saber graficar fracciones en la recta numérica y por ello, te comparto el siguiente video.
CONCEPTO DE NÚMERO.
En el aspecto de concepto de número incluimos las representaciones de los números cuando éstos no están asociados a ninguna operación ni al orden. Es de esperar que esto suceda en el momento de introducir un nuevo sistema numérico, pero no únicamente ahí. Estudiamos si las representaciones en la recta se usan para “colocar los números” (representar los números de manera aislada) o como apoyo para “estimar”.
Figura 1 Representación de la recta para colocar puntos.
Además, diferenciamos si los números se representan con puntos o con flechas y si las rectas usadas son horizontales, verticales o ejes cartesianos.
Figura 3 Representación de una suma con puntos-flecha
Figura 4 Representación de una suma con tres flechas.
SUMA Y RESTA.
En la suma y resta distinguimos si las representaciones utilizadas son del tipo puntos-flecha (véase figura 3) o del tipo tres flechas (véase figura 4). En ocasiones estas representaciones pueden venir acompañadas de un problema aditivo verbal. Por ello, también distinguimos el tipo de estructura de problema a la que se asocian. Los problemas aditivos que hemos analizado son los siguientes, adoptando la notación de Bruno y Martinón (1997):
• Cambio: ei + v = ef (estado inicial + variación = estado final). “Un delfín estaba a 5 metros bajo el nivel del mar y bajó 8 metros. ¿Cuál era la posición del delfín después de este movimiento?”
• Combinación: e1 + e2 = et (estado parcial 1 + estado parcial 2 = estado total). “Pedro tiene 8 pesetas y debe 15 pesetas. ¿Cuál es su situación económica total?”
• Dos cambios: v1 + v2 = vt (variación primera + variación segunda = variación total). “La temperatura bajó 11 grados y luego subió 5 grados. ¿Cómo varió la temperatura con respecto a la que hacía antes de moverse?”
• Comparación: e1 + c = e2 (estado menor + comparación = estado mayor). “Un coche está en el kilómetro 6 a la izquierda del cero y una moto está 11 kilómetros a la derecha del coche. ¿Cuál es la posición de la moto?”
PRODUCTO.
Para el producto distinguimos si las representaciones que se utilizan son de sumas reiteradas (véase figura 5) o bien de producto cartesiano (véase figura 6). Igual que en las sumas y las restas, estas representaciones pueden aparecer contextualizadas con problemas de multiplicación o división. Distinguimos si los problemas que aparecen son de:
• Razón: “Tengo 42 sillas que quiero colocar en 7 filas del mismo tamaño. ¿Cuántas filas podré formar?”
• Comparación: “Juan tiene 23 años y su abuelo tiene tres veces la edad de Juan. ¿Cuántos años tiene el abuelo de Juan?”
• Producto cartesiano: “Tengo 4 blusas y 5 pantalones. ¿De cuántas maneras distintas me puedo vestir?”






No hay comentarios.:
Publicar un comentario